Distortion noun /dɪˈstɔːr.ʃən/ — A change to the intended or true meaning of something; a change to the original or natural shape of something; a change in or loss of sound quality, due to changes in the shape of the sound wave. (Cambridge Dictionary)
Framing distortion
Distortion entails some kind of re-representation of something by changing its shape. Molding it through deformation. Bending it to create a new perspective. By changing shape, distortion introduces new interpretations, emphasizing certain aspects while downplaying others. Unlike abstraction or filtering, distortion inherently warps structure. It is not simply change; it is, by its very nature, a deliberate structural deformation. This fundamental characteristic sets distortion apart from abstraction and filtering. Abstraction is an act of generalization to gain broader, contextual understanding. For instance, Singular Value Decomposition (SVD) is a method of abstraction; by reducing the dimensionality of the data, the representation is simplified, but the original structure remains intact. It aims to lower the structural fidelity without distorting it.
In 3D modelling, an analogous action would be to decimate: to reduce the number of polygons of a mesh while minimizing shape changes. Although the shape will change, reshaping is not the intention of the algorithm. In descriptive statistics, an example would be deriving and using means in place of original values; not aiming to distort, only abstract. Filtering omits certain elements and narrows the representation, but does not alter the remaining structural parts. For instance, when filtering rows in a dataset, the remaining items stay unaltered, retaining their original structure and relationships. Unlike distortion, it does not reshape or bend the underlying meaning. It simply excludes parts.

The primary means to communicate information includes visual, auditory and physical mediums. Optical distortion involves reshaping or bending light waves in some way, as in the case of a microscope; microscopes magnify details by bending light through a lens. Sound distortion implies a change to the shape of the sound wave itself. In music, guitar distortion originates from increasing the volume beyond what the speaker can handle. Since the speaker cone is physically constrained from moving the required distance, the sound wave is compressed at its peaks, producing a distinct aggressive tone. Mediums such as these exist in physical space, and so do their distortions.
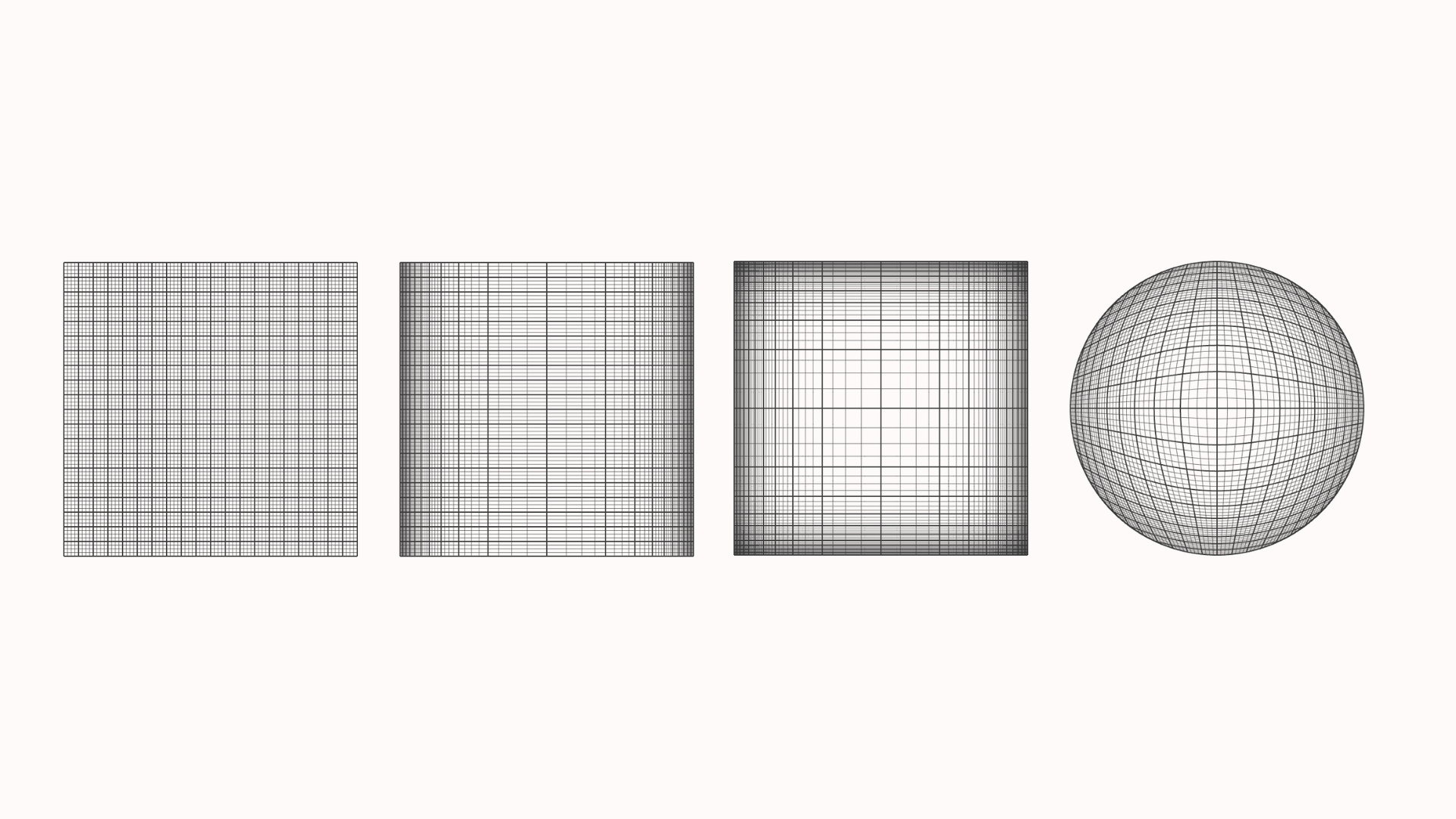
In visualization, space exists purely as a construct, allowing designers to bend, displace and collapse it in ways that would be impossible in reality. For instance, virtual space can be bent by applying modifiers to the representation of the spatial domain. In physical reality, achieving the same effect would require manipulating the fabric of space-time itself, something only achievable by extreme physical phenomena, such as black holes. This gives god-like powers to the designer, and with great power comes great responsibility.
In visualization, distortion primarily manifest in two ways: by bending space, or by reshaping the data. Bending space involves altering the spatial domain, such as mapping input values to a logarithmic scale, effectively reshaping the environment in which the data resides. Reshaping the data, on the other hand, involves transforming the function/value domain, such as applying a logarithmic transformation to the output values, which changes the data itself while leaving the underlying space unaltered.

In visualization, bending space is a common method to emphasize areas without altering the underlying data. For instance, fisheye views magnify areas of interest while compressing the surrounding area. In three dimensional visualization, a special case of distortion occurs when projecting onto two dimensions. One might compare it with dimensionality reduction in SVD, and ask: is projection an act of distortion or abstraction? I think it is both. It abstracts by reducing a three-dimensional scene to a two-dimensional representation. At the same time, projection is designed to simulate light traveling through virtual space. By altering the projection, one can simulate optical distortions, such as the bending of light waves through air, materials, and our eyes. This already poses a distortion dilemma: which projection should one choose? One that emulates how humans perceive the world in perspective, or one that project space orthogonally? Arguably, perspective projection introduces more distortion mathematically, still, orthogonal projection appears more distorted to the human eye.
The good, the bad, and the ugly
Although changing the true meaning of something might seem counterintuititve when searching for the truth, in some cases, distortion is strictly necessary. Take the microscope, for instance: distortion is what makes the phenomenon visible in the first place. In other cases, distortion might not be strictly necessary but is used to enhance comprehension by emphasizing features or changing perspective. However, distortion is a double-edged sword. While it can enhance comprehension, it can also mislead when applied badly. This raises ethical considerations about the way distortion is used, especially in scientific communication.
Good use occurs when distortion improves perception without misleading. Bad use can be unintentional, such as poor design choices. Bad use can also be intentional, such as deliberate manipulation to exaggerate certain narratives. Intentional misuse of distortion (the bad) is ethically inexcusable, since it deliberately seeks to mislead. Unintentional misuse (the ugly), while perhaps more ethically excusable, might still lead us astray on our path towards truth. The boundary between bad and ugly is often blurred; one can always claim actions was unintentional, even when deliberate. This complicates the ethical landscape. Ultimately, regardless of intent, the harm lies in the result: when distortion misleads, it betrays the trust of the audience and compromises the integrity of all science. Therefore, designers have a responsibility to ensure their distortions are aligned with the pursuit of truth.
In the paper “Graphs with logarithmic axes distort lay judgments” by Ryan et al. [9], the problem of misunderstanding exponential growth is explored in an empirical study. It shows, using examples of Covid-19 data, how the choice of a linear or logarithmic scale on the function axis impacts the perception of growth. They demonstrate that logarithmic scales, while useful in research, often lead to less accurate judgements among lay audience. Participants viewing logarithmic scales were more likely to underestimate the severity of the pandemic, perceive Covid-19 as less dangerous, and express less support for interventions such as mask-wearing and social distancing. While logarithmic scales are important tools in research, one needs to be careful when presenting them to the public. As Ryan et al. suggest, the communication of such graphs should ideally include clear explanations, or be supplemented with linear representations, to lower the risk of misunderstanding.
A common trick with barcharts is to truncate the length-axis, effectively zooming in on a portion to exaggerate the differences in bar lengths. Whether this should be considered distortion or not is an interesting question: The remaining scale is not altered, so are we not simply filtering out irrelevant portions of the axis? This would be true for a dot plot, since points do not have lengths that can be altered. However, in bar charts, the length of a bar is conceptually significant. It stretches all the way to the start of the axis. By truncating the length-axis, you are effectively compressing the omitted section into an infinitely small area, fundamentally distorting the function domain.

In “How Deceptive are Deceptive Visualizations” by Pandey et al. [7], truncating the length-axis falls under the category of message exaggeration. While the actual data remains unaltered, the manipulation of visual encoding exaggerates the perceived magnitude of differences, misleading the viewer into overestimating the variation between data points. To help visualization creators avoid unintentional distortions, the authors advocate for principles and guidelines that promote best practices. For lay audiences vulnerable to intentional distortions, the authors highlight the importance of education to enhance their ability to recognize problematic and potentially deceptive information.
In visualization research, two-dimensional view distortion techniques have received a lot of attention. These techniques aim to address the challenge of presenting large, complex datasets within constrained areas. By selectively magnifying regions of interest while compressing the rest, view distortion techniques allow users to focus on details without losing contextual information. Inspired by effects from cartography and photography, such as the fisheye lens, these techniques distort space to highlight important information.
In “A Review and Taxonomy of Distortion-Oriented Presentation Techniques” [2], Leung et al. identify good and bad uses of view distortion techniques. On the positive side, view distortion can enhance comprehension by dynamically allocating screen space to areas of interest. For instance, in cartographic applications, distortion can allow users to zoom into densely detailed regions while retaining an overview of the surrounding geography. On the negative side, distortion can mislead users by overemphasizing less important areas, causing them to appear more significant than they are. While Leung et al. does not express any ethical concerns in their paper, they emphasize the importance of clarifying what is distorted and what is not, to make sure the audience remain unbiased. Ethical concerns around view distortion are especially relevant in cartography. For instance, as discussed in “How to Lie with Maps” by Monmonier [1], map projections like the commonly used Mercator projection distort the relative sizes of countries, making regions near the poles appear much larger than they are in reality. This can strengthen cultural or geopolitical biases, influencing the audience’s perception of importance or power. Because the Mercator distortion is not typically explained explicitly on maps, it risks manipulating entire populations into adopting a skewed worldview.

Although less common, spatial distortion in three dimensions has its uses. As described in “Exploring Large Graphs in 3D Hyperbolic Space” by Munzner [4], hyperbolic space allows massive datasets to be visualized in a compressed area. By magnifying space around a focus node and its immediate connections, while compressing distant regions, it helps users enhance details without losing sight of the overall graph.
In “Spatial Transfer Functions — A Unified Approach to Specifying Deformation in Volume Modeling and Animation” by Chen et al. [6], spatial transfer functions are used to deform 3D volumetric objects. This enables transformations such as sweeping, stretching, and twisting of spatial fields, facilitating interactive exploration of volumetric datasets. As with any distortion technique, these require careful implementation to avoid confusion. Being very technical, they might demand even greater attention to detail compared to simpler methods. However, ethically, there is probably less likelihood of intentional misuse. These techniques are highly specialized and are not typically used in contexts where they might influence public opinion. Their primary focus is on enabling exploration of complex data for specialists, rather than persuasion or public-facing communication.
A more common way to distort in two- and three-dimensional visualization is through non-linear color mapping. Color mapping is a widely used technique in visualization, where a one-dimensional value space is mapped to a continuous range of colors. This lets users see relative differences in data. However, if the values span several orders of magnitude, a linear mapping might be ineffective in displaying detailed differences. To address this, the value space can be mapped onto a non-linear scale, such as a logarithmic or exponential scale, before the color interpolation is applied. Logarithmic mapping details smaller values by expanding their range, while compressing larger ones, and exponential mapping does the opposite, expanding larger values while compressing smaller ones. It is also possible to bend space around a particular value, in effect applying a lens-like distortion to an interval, to better detail the differences around that value. This could be beneficial for normally distributed values, or other distributions with curved shapes. The use of non-linear color mapping can be very useful when applied appropriately, but it can also lead to misleading interpretations when it is not.
As Monmonier highlights in “How to Lie with Maps” [1], the choice of scaling and color scheme can manipulate perception, and designers of such visualizations have an ethical responsibility to ensure their design choices do not compromise the audience’s understanding of the data. This does not mean linear color scales are inherently the more accurate or undistorted choice. For instance, when visualizing percentage changes in a population ranging from -100% to +100% on a choropleth map, it might be more suitable to use a non-linear color map. This is because decreases and increases are not linearly proportional: a -50% change (halving the population) is equivalent in magnitude to a +100% change (doubling the population). A linear scale does not show this balance, making decreases look smaller than similar increases. As explained in a tweet by D3 inventor Bostock [8], a diverging logarithmic scale makes sure changes in both directions are shown equally. However, I think that since understanding such a scale might be challenging for lay audiences, using descriptive terms like half and double in addition to numerical values like 0.5 and 2.0 could add to its intuitive interpretation.

Conveying the mechanism
These examples barely scratch the surface of what is possible with visualization. The virtual world offers limitless potential, unconstrained by the realities of our physical world. Designers possess the power to manipulate space and form, bounded only by their imaginations. As noted earlier, with such power comes a great responsibility to prioritize the pursuit of truth. In “Is Science Losing its Objektivity?” [3], Ziman writes: “scientists are united in `the pursuit of truth’. But some philosophers say that `truth’ is an illusion, whereas others say that it takes many forms….”. This raises the question: if truth is subjective, an interpretation unique to every person, how can we define a unified path towards it? Everyone has their own truth, their own narrative of the world. Should visualizations only align with the audience’s existing truth, reinforcing their current worldview? Or should it aim to challenge their truth, reshaping their perception of reality? The latter inevitably involves manipulation, as it pushes the audience toward a narrative that conflicts with their existing truth. If a visualization inherently alters subjective realities, can it ever avoid biasing? Is attempting to change someone’s truth manipulative, or is it simply part of the process of teaching?
We must accept that engaging in science involves both producing and receiving new narratives. Our worldviews, our subjective truths, will inevitably change as a result of knowledge sharing. This is a fundamental aspect of learning and growth. What is important, however, is recognizing how our worldview is being changed, as it happens. Equally important is our responsibility to convey transparently and accurately to others how we are trying to shift their perception, so they can recognize how their worldview is being reshaped. Any distortion is ethically defensible in principle, as long as the audience clearly understands its underlying mechanisms and how it is altering their perception of the world. This aligns with the recommendations in the referenced studies: if a distortion feels ethically conflicting, rather than entirely excluding it, ensure its mechanisms are thoroughly and transparently conveyed. If, despite thorough explanation, the intended audience still cannot grasp its inner workings, then the ethical responsibility shifts to reevaluating whether the distortion is appropriate at all.
Ultimately, in knowledge sharing, the truth is the opacity of the medium engine itself. Whether it relies on abstraction, filtering, or distortion, the clarity of its mechanism determines its ethical integrity. When the mechanism is obscured, the result is manipulation: information transfer without transparency.
References
1. Monmonier, M.
How to lie with maps
University of Chicago Press (1991)
2. Leung, Y. K. & Apperley, M. D.
A review and taxonomy of distortion-oriented presentation techniques
ACM Transactions on Computer-Human Interaction (TOCHI) 1, 126–160 (1994)
3. Ziman, J.
Is science losing its objectivity?
Nature 382, 751–754. issn: 0028-0836 (Aug. 1996)
4. Munzner, T.
Exploring large graphs in 3D hyperbolic space
IEEE computer graphics and applications 18, 18–23 (1998)
5. Cambridge Advanced Learners Dictionary and Thesaurus
Cambridge University Press (1999)
6. Chen, M., Silver, D., Winter, A. S., Singh, V. & Cornea, N.
Spatial transfer functions: a unified approach to specifying deformation in volume modeling and animation in Proceedings of the 2003 Eurographics/IEEE TVCG Workshop on Volume graphics (2003), 35–44
7. Pandey, A. V., Rall, K., Satterthwaite, M. L., Nov, O. & Bertini, E.
How deceptive are deceptive visualizations? An empirical analysis of common distortion techniques in Proceedings of the 33rd annual acm conference on human factors in computing systems (2015), 1469–1478
8. Bostock, M.
Twitter Post: https://x.com/mbostock/status/991517711250305024 (2018)
Accessed: December 5, 2024.
9. Ryan, W. H. & Evers, E. R.
Graphs with logarithmic axes distort lay judgments
Behavioral Science & Policy 6, 13–23 (2020)

Marius Irgens
I am currently a PhD student at the University of Oslo, researching Data Visualization methods on the topic of Technical Debt.
I have a bachelors degree in Computing from Western Norway University of Applied Sciences, and a masters degree in Informatics with specialization in Data Visualization from the University of Bergen.
I work alot with C++, OpenGL and Javascript. I love graphics, data analysis/visualization and system design.