Colorless Green Graphs Sleep Furiously: A Conversation with Leland Wilkinson

This article traces some history of ideas behind Leland Wilkinson’s development of the Grammar of Graphics (and later, of ggplot2) in the form of a discussion / debate between Lee and the author. At issue were meta-questions of data visualization: (a) the essential nature of software for data graphics; (b) the idea of a comprehensive, mathematical theory for graphics expressed in computer syntax; (c) the idea that there is something beyond syntax in the code of data graphics. 

Introduction

In 2017, for the Joint Statistical Meetings in Baltimore, I organized an invited session on The Development of Dynamic and Interactive Graphics, with Luke Tierney and Dan Carr as featured speakers. Afterwards, I met several other friends for dinner at Azumi on the inner harbor.  Present also were Howard Wainer, Lee Wilkinson, Paul Velleman, and others. The inventive (if overpriced) Japanese cuisine that was served was so visually appealing and provided a backdrop for a wide-ranging discussion of data visualization. 

In the course of the evening I got into a discussion (or debate) with Lee about the wider understanding of data graphs and implementations of graphics in software systems. Lee’s main point was that the Grammar of Graphics (GoG) was a complete, self-contained mathematical theory of statistical and scientific graphics. He meant this in the sense of a formal grammar, such as Chomsky’s (1957) Syntactic Structures, that could produce any well-formed, syntactically correct sentence in a language and could not produce any syntactically incorrect ones. 

I countered that there was more: the semantics or meaning of graphs and poetics—the beauty of the language of the code that was used to create a given graphic, the connection between the idea of a graph and the language used to create it on a computer. As one example, I used “Colorless green graphs sleep furiously,” a paraphrase of Chomsky’s famous example of a sentence whose grammar is syntactically correct and whose meaning is nonsensical semantically, but could have an appealing poetic interpretation. 

After that dinner, I proposed that we write a joint article summarizing some of these issues, but neither of us had the time to pursue this. What follows is a lightly edited transcript of our follow-up discussion, with the goal of exposing what Lee and I were thinking at that time, more explicit than has previously been expressed in print. It concludes with a coda intended as tribute to Lee. It is not an overstatement to say that Lee was among the most profound thinkers in modern data graphics. His Grammar of Graphics  (Wilkinson, 1999) revolutionized theory and practice and is now the basis of most modern graphic software systems. 

Letter from Lee, August 8, 2017

Thanks for the invitation to co author an article on some of the topics we discussed. While needing to decline, I nevertheless think I ought to clarify some of the points that were possibly the source of misunderstandings. Many of those misunderstandings didn’t surprise me because I’ve seen them pop up occasionally in comments on Grammar of Graphics (GoG). It’s been difficult for some readers to relinquish a popular nostalgia for what one reviewer called “the golden age of statistical graphics.” That “golden age” was described as spanning books by Bertin, Cleveland, Tufte, Wainer, and others. As I mentioned in my reply to that reviewer, however, GoG doesn’t belong on that bookshelf. GoG has nothing to do with those books or, for that matter, with any writing on the efficacy of various visualizations, good usage, taxonomies, history of graphics, new types of graphics, semiotics of graphics, storytelling with graphics, human perception of graphics, or the mind’s eye.

So, what is GoG concerned with? As I explained in the book, it involves the mathematics underlying statistical and scientific graphics. I am interested in any graphic that can be expressed in an explicit mathematical model. That model induces a huge corpus of graphics that were, prior to GoG, considered to be disparate.

Why do I think a mathematical model of graphics is important? Because GoG invokes a new world of visualization. It is not a world of printed graphs or even a world of interactive exploratory systems like XGobi, JMP, or DataDesk. Instead, it is a world where a computer understands the content of a graphic.

Consider the following illustrative collection of use-cases in that world.

1. “Here are some data. Please analyze these data and show me the kind of interesting things an expert in visualization would find.”
2. “Here is an image of a published chart. Please parse this image, extract the data from it, and generate an equivalent chart in the style of Cleveland, Holmes, or Tableau.”
3. “Here is a table of results from a factorial experiment. Please fit a plausible subset model to these data and show me a graph of the residuals in each cell of a similarly formatted table.”
4. “Here are the dates, temperatures, divisions, and coordinates of Napoleon’s march to and retreat from Moscow. Draw Minard’s map, highlight the date of the minimum temperature, and explain its effect on the number of surviving troops. Also, tell me the average speed (in kilometers per hour) of the troops as they marched.”

I assert that there is no system not based on GoG that can implement these tasks. No amount of hand-waving can substitute for mathematics when you program a computer.

Now, the points I’ve made so far in no way denigrate or exclude the important investigations of history of graphs, visual processing of graphs, memory for graphs, design of graphs, and so forth. I am only saying that these ideas cannot be used to train a computer to understand a graph. They are germane to standards of graphics usage, to design of effective UI’s, etc.

When I told you at dinner that I don’t care whether a particular graph is popular or not, however, that’s because the question is irrelevant to understanding the structure of a graph. In fact, one of the most popular graphs is the Pareto Chart. As I showed, this popular chart is ungrammatical or, equivalently, ill-formed. It rests on a mathematical mistake.

When a graph has a clear GoG structure, then there is little use in trying to express that structure in some other way. Conversely, GoG structure has nothing to say about aesthetics, effectiveness, or other non-mathematical aspects of a graph.

There are two dimensions to GoG. The first is temporal. As this figure from the book shows, the construction of a graph is a total order — one cannot do these tasks in a different order and get a correct graph. That’s a strong statement; one I haven’t seen refuted. In fact, I exposed serious bugs in Tableau because they failed to observe this ordering.

Unfortunately, this figure has been taken by some to be an ordinary data flow. But data flows have little to contribute to the understanding of graph construction, despite their widespread use in describing such things. By contrast, this figure represents a function chain. Each class contains functions (methods) that are composable. The expressiveness of GoG is due to this composition; each class has many methods and the repertoire of graphs produced is a product set of all these methods. I have seen no other graphics platform, including D3, SAS, R, or even SYSTAT that can produce as wide a range of graphics as nViZn.

Lamentably, one reviewer failed to notice that this figure is an outline and sequencing of the chapters of the book. It is a description of the actual objects (classes) used in the GoG program called nViZn (now called IBM RAVE). This reviewer thought the book’s organization to be rather haphazard and ad hoc. This signaled to me that the reviewer completely misunderstood the logic of GoG and thought the topics covered were simply independent aspects of visualizations. In the almost two decades of GoG, the only group I’ve seen that understands GoG in detail is engineers responsible for producing major graphics systems— the engineers at R (ggplot2), Python, Microsoft, Google, Tableau, Facebook, and Netflix. That’s where the book is still selling — in numbers that increase each year.

The second dimension to GoG is structural. Here is a graph diagram of the whole system. It was produced by dragging the Java package directory into AutoViz — using GoG to analyze GoG. Notice that the classes in the figure above are actually represented in the Java code. 

[MF: I omit this network diagram here. It shows that the structure of the nViZn code for GoG closely matches the diagram in Figure 1, but shows the functions involved in each class.]

Minard graphic

Now let’s take a look at the Minard graphic. Here’s the structure of that graphic. It was produced by dragging the XML used to produce Minard in nViZn. I hope you see that there’s a fundamental difference between demonstrating the structure of Minard using an explicit executable specification vs. explanations in ordinary language or miscellaneous collections of graphics primitives (point, line, area, text, etc.).

[MF: I omit this diagram here.]

When I described the fourth use-case above (interpreting the Minard graph), I had in mind this graph of the elements in the XML. Each class in GoG can have methods that answer questions about that class. Thus, temperatureGraph has information about its scale and other attributes. By the use of introspection and reflection and extension, languages like Java can add other capabilities to classes without recompilation. But these additions need not involve specific customizations for every visualization, because GoG is object-oriented rather than functional.

Now let’s look at the code. The following is the formal Graphics Production Language that draws Minard when submitted to the nViZn interpreter in SPSS.

The blue section is simply a data specification. The actual graph specifications are in black. Now, you should compare this not only to the other programs’ sizes (orders of magnitude more prolix), but also to their ill-formed and ad-hoc organization. Programs that simply draw primitives (lines, areas, text, etc.) are not to be compared to a language like nViZn that is grounded in graphics objects. This is why I urged you not to waste your time reviving the Minard contest. Plenty of things can be programmed on a computer, but the resulting code doesn’t necessarily tell us anything about the meaning of what is produced. Every engineer recognizes spaghetti code. The other Minard programs are simply spaghetti.

Here is the result:

I hope this answers some of the questions you had and clarifies the source of some of the disagreements. I’m especially concerned that nobody thinks GoG is a “theory” or a “taxonomy” or a “platform.” GoG is a mathematical system, and arguments against it (or relativizing it) need to be made on a mathematical basis. I’m not at all interested in whether someone draws the Minard map (one can do that best with Adobe Illustrator) or makes beautiful visualizations like D3 or Mathematica. GoG is about formulating the meaning of a graphic in a way that a computer can understand enough to draw it and answer questions about it.

Reply to Lee, August 25, 2017

I don’t really have time either to pursue an article such as I proposed (although it would be fun) but let me make clear that I agree with most of what you say. In fact, I strongly believe that the power of “GoG” theory is that it provides a coherent mathematical model for statistical graphs, and as you say, the key thing is that, in some sense, the language allows the computer to understand — and as actual proof, produce the content of a graphic.

That is the true power of the GoG approach for me — the clear arrangements of the steps from data to a finished graphic, each with its attributes and components, and also the ideas that steps have a clearly defined temporal order, and one can see violations of the grammar as a consequence of ignoring some of its features. This is brilliant, but my main point is that it only goes so far.  

(I’ll leave aside as unnecessary and unproductive here the question of uniqueness — are there other distinguishable, but functionally equivalent graphics postulates? Like a different set of axioms for some geometry.)

Implementation matters

I think we differ on the question of implementation — GoG can be implemented in a variety of different computer languages that are not all equivalent from my perspective. You say that only the mathematical description of a graph in GoG is important. I say that there is more.

Even if different implementations are functionally equivalent to a computer and produce identical results, some software language implementations can be considered more expressive than others, in that:

• Expressive power: ease of translating what you want to do into the graphic output you want
• Elegance: the code can be “read” by a human in a more (or less) comprehensible way, one that offers more (or less) insight into the relation between the graphics specification language and the code, or 
• Extensibility: code can be more (or less) easily extended to encompass additional aspects of the process of composing a graph in a common language.

 I see this as a separate issue from that of the mathematics behind the theory, but an important one that should not be dismissed. The mathematical aspects of GoG provide the theory; implementations define the practice.

A prime example comes from my ancient work with Logo, where the language features of recursion, list processing, etc. (inherited from Lisp, with sufficient syntactic sugar) made it a delight to understand the structure of complex Moorish tiling patterns, trees, both real and abstract, etc. in their very simple language description (Friendly, 1988).  A square of size X wasn’t just a collection of four (x,y) points with constant shifts, but rather the simple path of a turtle doing 

REPEAT 4 [FORWARD :X RIGHT 90]. 

That simple change in frame of reference for a computer language from Cartesian coordinates to Turtle-centric coordinates made it possible to introduce young children to what Seymour Papert called “Powerful Ideas” in Mindstorms (Papert, 1980).

One simple illustration: A spiral is the path of a turtle going [FORWARD :size RIGHT :angle] and then doing the same with a slightly larger value:

Children are delighted to see that a small change from a square spiral makes an artistic image.

I also argue that the implementation of ggplot2 and its extensions is both a testament to the power of GoG and also a way to make the specification of a wider array of graphs much easier to actually specify in a largely coherent syntax.  I am not knocking the nViZn implementation at all, but I better love the idea of plots as composed of multiple layers, connected by “+” signs in ggplot2. To a human, this is much easier to read and write than the nested function calls of nViZn.

Another part of this is a codification of the process of ideas about data manipulation in terms of manipulating cases (filter, sample, sort, …) or variables (select, combine, transform, mutate), grouping/aggregating and multi-table, SQL-like constructs.  I know that a lot of this is implicit in your Chapter 5 on Algebra of data, but I don’t know of any implementation of this.  

The R implementation probably differs from what you may have been thinking. The features for data manipulation (dplyr), data import (readr), handling dates (lubridate), strings (stringr), databases (DBI), foreign files from SAS, SPSS, … (haven), are becoming increasingly coherent.  But one key feature is the powerful idea of a data pipeline, in which a graphic call can be an element of the chain. This is not at all new in CS: it goes back to Kernighan & Ritchie and unix pipes (“|”), now implemented in R with “%>%” syntax.  But the combination is greater than the sum of its parts.  

For a wider appreciation of the idea of “implementation matters”, the website 99 Bottles of Beer gives 1,500 different program language implementations of the song, 99 Bottles of Beer, not a great test case, but at least it illustrates the range and expressivity of different language paradigms. All do the same thing, but some languages do it  more elegantly.The Tower of Hanoi problem is another that has attracted implementations in a wide variety of programming languages, but I don’t know of any comprehensive collection.  I still like my Logo version in Advanced Logo (Friendly, 1988):

Reading the code is all you need to know if you understand recursion.

A key feature of this way of thinking was that the MOVE function could be anything: it was the only part that determined the “output”— it could:

• simply print “Move disk 1 from Tower A to B”,  
• draw the effect on a screen in various ways, 
• instruct a robot arm to actually pick up a disk and move it, or 
• draw a tree diagram reflecting the history of all moves from the start to a solution.

On my Ubuntu development server, I have Xscreensaver in my startup, and one of my favorites is a 3D open GL version that renders the HANOI process with an arbitrary number of disks, animated to rise from a peg, and rotate in 3D several times before it lands on the destination peg.  All of this while the entire scene is also rotated in the XY plane, with lighting and shading applied to all the disks and pegs.  Expressive power, elegance, and extensibility are all rightful criteria for comparing graphics programming languages.

Minard

You took issue with my idea that Minard’s graph could still be used as a test case for comparing different graphic programming languages, or— my larger thought, that it could inspire people to think about what Minard wanted to say–and create other graphics to try to tell other aspects of the story.The fact that Minard’s graphic can be reproduced in spaghetti  code (such as graphic systems based on points, lines, areas, text primitives) doesn’t say that there are not other, principled and informative ways to draw this graphic. As a test case, I tried to do a better job than I had done before with ggplot2 in R. The code for this figure is in a github gist.

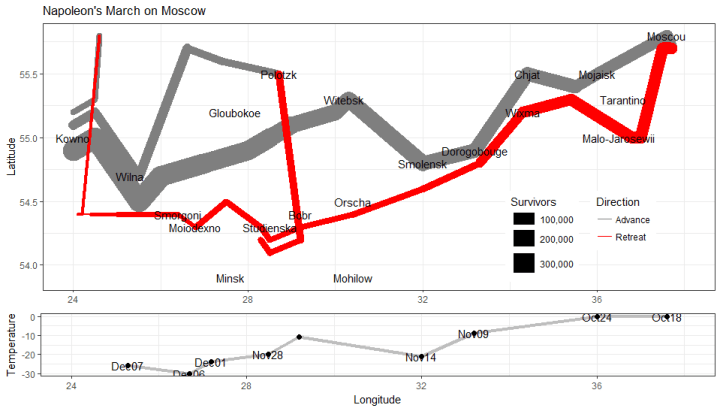
What I learned from this little exercise is that, as you say: the devil is in the details. Or when I invoke the 80-20 rule:  I could get the basic 80 percent form right with 20 percent of the code and effort, but the graphic details took the remaining 80 percent of effort, and I don’t regard this as a finished product—certainly not to Minard’s standards.  

But another point here is that to say that the idea that a graph such as this can simply be reduced to the mathematical specification of GoG or in ggplot2 notation misses the point that there is a lot of human judgment that goes into the use of aesthetics, plot annotations, etc.  

The main area where we disagreed, at dinner and now, had to do with my point that there is much more to a statistical graphic than can be captured in the GoG, and that has to do with human understanding and the purpose for which graphs are drawn.  Minard designed his wonderful graph to tell a particular and poignant story about the folly of leaders who would sacrifice so many for their own glory.  That part, which is poetry (Friendly & Wainer, 2021), cannot be captured in a mathematical theory of graphs, even if one can reproduce it in an elegant syntax.

Coda

Looking back at this discussion four years later, it doesn’t seem we differed as much as I made out. Our beliefs and values about data graphics largely overlapped. It was more a matter of emphasis. Lee was correct that GoG was as close to a complete mathematical theory of data graphics as has ever been conceived. I was talking about a different aspect, more to do with the beauty of code as a mental pipeline to take the idea of a graph and produce what you want with as direct a connection between the idea and the result as possible. 

In the history of data visualization, there are some events that stand out as more general and influential, beyond some exquisite and beautiful, but specific, examples. Playfair’s constructions of nearly all the modern forms of data graphics around 1800 (line chart, bar graph, pie chart) is one such event we celebrate as the “Big Bang” of data visualization. The next signal event came with Jacques Bertin’s (1967; English translation: 1983) Semiology of Graphics, which laid the framework for a comprehensive system of visual signs and their meanings to synthesize general principles of graphic communication.

But Bertin’s schema was conceptual, not computational. Like many verbally stated theories (famously, Freudian theory), there was no direct way to test, prove, or refute the assumptions or conclusions from Bertin’s system.  The Grammar of Graphics changed all that. Wilkinson asserted that GoG could produce any well-formed, syntactically correct graph, even those that had not yet been invented; perhaps more contentious was his claim that the strict framework of GoG could not produce any syntactically incorrect ones. 

The beauty of a computational specification of data graphics is, first, that the software can provide automatic equivalents of spell checking and grammar checking for text by throwing an error for any syntactically incorrect graph. The second, semantic checks are more varied and not easily automated: you can easily see if a kind of graph “works” or not by running test cases, just as mathematicians try to challenge a theorem by proposing a counterexample. The proof is in running the code! 

GoG has become the de facto standard conceptual structure for software implementations of data graphics, perhaps not in the strict pipeline shown in Figure 1, but certainly in terms of the ideas of layers, aesthetics, scales, stats, geoms, and facets. GoG ideas made their first appearance following Wilkinson’s initial SYSTAT package. In this, he tried to be able to reproduce nearly any graphic he had seen before. Some higher-level ideas became apparent, e.g., that histograms and Nightingale rose diagrams differed only in using cartesian vs. polar coordinates.

Around the time that SYSTAT (1995) was acquired by SPSS, Lee and others had developed the initial specifications for what would become the Graphic Production Language (GPL), which embodied what would become the GoG and was implemented as the underlying machinery for SPSS graphics. In 1996, Lee and Dan Rope developed nViZn as a set of Java classes (see the essential ideas here.) All the essential ideas of GoG are present in the data flow diagram they used to explain the system (Figure 4). 

Shortly thereafter, Lee teamed up with Graham Wills to take the nViZn Java classes to a Whiz-Bang demonstration project. They created a Java application (a .jar application) called AutoVis (Wills & Wilkinson, 2010). When launched, it presented a box saying, “Visualize Me.” As proof-of-concept, you could drag and drop nearly any kind of object onto the box. Standard things like tables or spreadsheets were easy, but you could also drop the text of Moby Dick and see a network diagram of all the main actors. AutoVis is now an active Python project.

In a nearly coincident step, Hadley Wickham initially wrote the ggplot package for R in 2008, translating Wilkinson’s framework into the object-oriented structure for R.  But to my main point, the implementation syntax clearly did not work cognitively: plots used nested function composition, like h(g(f(x))),  as in ggpoint(ggplot(mtcars, list(x = mpg, y = wt))). This syntax was perfectly understandable to a computer, but like LISP was challenging for a human ( To counteract, code editors like emacs developed brace matching and indentation schemes.  LOGO was actually based on LISP, but with the change in syntax it was called “LISP without tears.”)

The result was a completely new implementation, ggplot2, using a formal, algebraic representation of layers as ggplot objects joined by ‘+’ (Wickham, 2010). This redesign also hewed closer to the formal GoG framework of stats, geoms, coordinates, scales, and aesthetics, all with sensible functions and inheritance of defaults.

After that time, the essential ideas of Wilkinson’s GoG (and it’s ggplot2 version) have formed the structure, and provided inspiration for implementations of data graphics in a wide variety of computer languages and software systems. Some examples are: Python (altair, plotnine); Javascript (Vega-lite, D3js, Observable Plot); Julia (gadfly). What is now Tableau Software began life as Polaris (Stolte & Hanrahan, 2000), structured around the GoG framework.  It is no accident that Wickham’s (2009) ggplot2 book was subtitled Elegant Graphics for Data Analysis. But there were several aspects of GoG that weren’t made explicit in the ggplot2 structure.  One was the idea of an Algebra for variables in the VarSet to be plotted, comprised of operators cross, nest, … to compose plotting variables from those in the input data set. Another important idea, but not shown explicitly in Figure 4 was that of the pre-processing that took place between the DataSource and the VarMap. This is now the subject of great development, called Tidy Data (Wickham, 2014) or the tidyverse in R. Lee would have been well-pleased with this. Data graphics today progresses so broadly because it stands on the shoulder of a giant.

---

References

Bertin, J. (1967). Sémiologie Graphique: Les diagrammes, les réseaux, les cartes. Paris: Gauthier-Villars, 1967

Bertin, J. (1983). Semiology of Graphics. Madison, WI: University of Wisconsin Press.

Chomsky, N. (1957). Syntactic structures. The Hague: Mouton.

Friendly, M. (1988). Advanced Logo: A Language for Learning. Hillsdale, NJ: L. Erlbaum Associates.

Friendly, M. and Wainer, H. (2021). A History of Data Visualization and Graphic Communication. Cambridge, MA: Harvard University Press.

Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.

Stolte, C. and Hanrahan, P. (2000). “Polaris: a system for query, analysis and visualization of multi-dimensional relational databases,” in IEEE Symposium on Information Visualization 2000. Proceedings,  pp. 5–14, doi: 10.1109/INFVIS.2000.885086 

Wickham, H. (2009).  ggplot2: Elegant Graphics for Data Analysis. Springer New York.

Wickham, H. (2010). A Layered Grammar of Graphics, Journal of Computational and Graphical Statistics, vol. 19, no. 1, doi: 10.1198/jcgs.2009.07098.

Wickham, H.  (2014). Tidy Data. Journal of Statistical Software, 59(10), 1–23. https://doi.org/10.18637/jss.v059.i10 

Wilkinson, L. (1999). The Grammar of Graphics. New York: Springer.

Wilkinson, L. (2008). The Future of Statistical Computing. Technometrics, 50(4), 418–435. http://www.jstor.org/stable/25471520

Wills, G. and Wilkinson, L. (2010).  “AutoVis: Automatic visualization,” Information Visualization, 9(1), 47-69.